Пример №6. Шарнирно-опертая балка
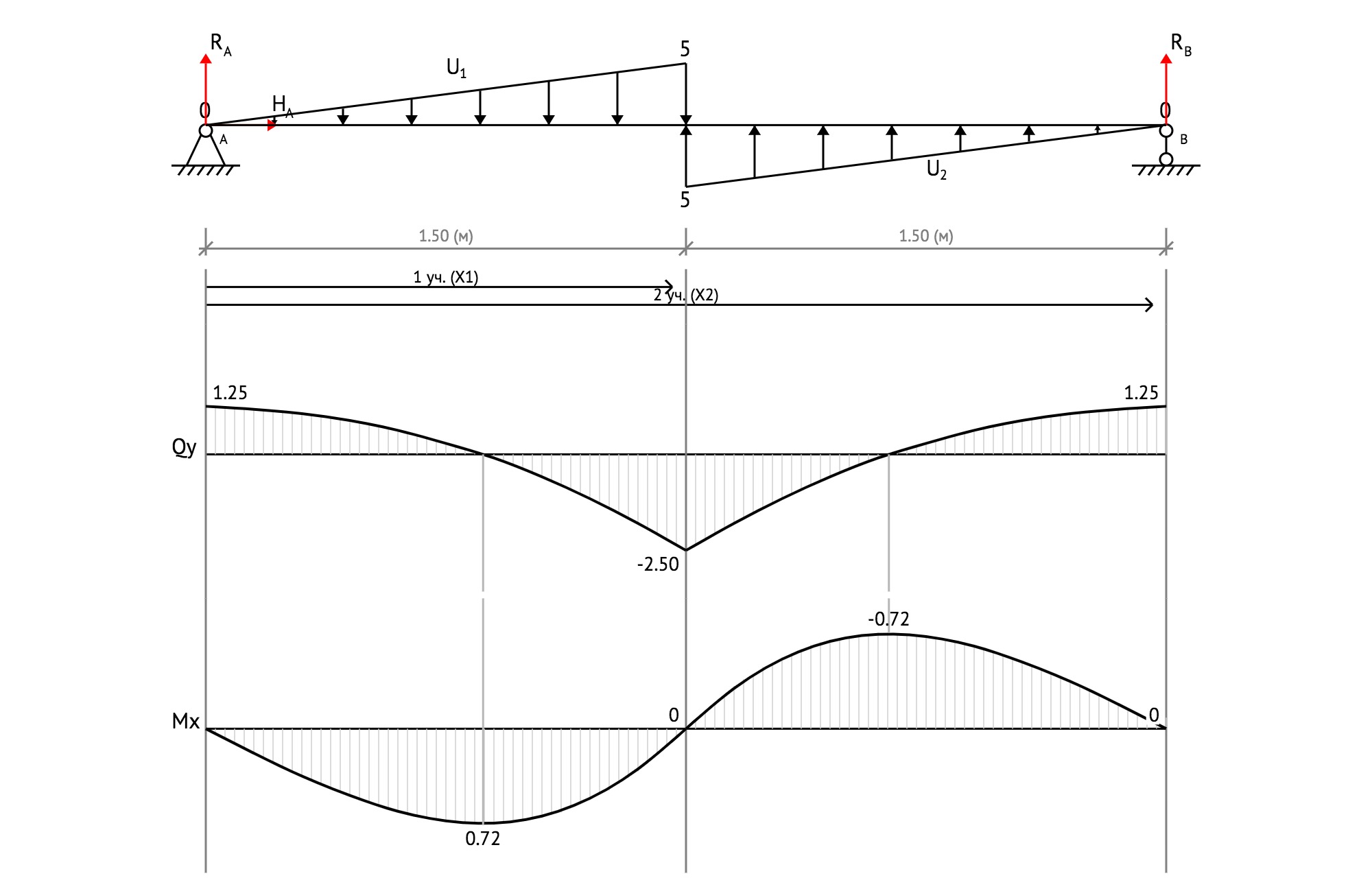
Определение опорных реакций
1. Согласно схеме решения задач статики определяем, что для нахождения неизвестных реакций необходимо рассмотреть равновесие балки.
ΣFx = 0: HA = 0
ΣMA = 0: Найдем сумму моментов относительно шарнирно-неподвижной опоры в точке A:
- (U1справа *1.5/2) * (1.5 - (1/3)*1.5) + (U2слева *1.5/2) * (3 - (2/3)*1.5) + RB*3 = 0
ΣMB = 0: Найдем сумму моментов относительно шарнирно-подвижной опоры в точке B:
- RA*3 + (U1справа *1.5/2) * (3 - 1.5 + (1/3)*1.5) - (U2слева *1.5/2) * (3 - 3 + (2/3)*1.5) = 0
2. Вычислим реакцию шарнирно-подвижной опоры в точке B:
RB = ( (U1справа *1.5/2) * (1.5 - (1/3)*1.5) - (U2слева *1.5/2) * (3 - (2/3)*1.5)) / 3 = ( 3.75 * 1 - 3.75 * 2) / 3 = -1.25 (кН)
3. Вычислим реакцию шарнирно-неподвижной опоры в точке A:
RA = ( (U1справа *1.5/2) * (3 - 1.5 + (1/3)*1.5) - (U2слева *1.5/2) * (3 - 3 + (2/3)*1.5)) / 3 = ( 3.75 * 2 - 3.75 * 1) / 3 = 1.25 (кН)
4. Решаем полученную систему уравнений, находим неизвестные:
HA = 0 (кН)
5. Выполним проверку решения, подставляя найденные значения в уравнение равновесия относительно оси Oy:
ΣFy = 0: RA - (U1справа *1.5)/2 + (U2слева *1.5)/2 - RB = 1.25*1 - (5*1.5)/2 + (5*1.5)/2 - 1.25*1 = 0
Построение эпюр
Рассмотрим первый участок 0 ≤ x1 < 1.5
Поперечная сила Q:
Q(x1) = + RA - (U1справа *(x - 0)/1.5*(x - 0))/2
Значения Q на краях участка:
Q1(0) = + 1.25 - (5*(0 - 0)/1.5*(0 - 0))/2 = 1.25 (кН)
Q1(1.50) = + 1.25 - (5*(1.5 - 0)/1.5*(1.50 - 0))/2 = -2.50 (кН)
На этом участке эпюра Q пересекает горизонтальную ось. Точка пересечения:x = 0.87
Изгибающий момент M:
M(x1) = + RA*(x1) + (U1справа *(x - 0)/1.5*(x - 0))/2*(x - 0)*(1/3)
Значения M на краях участка:
M1(0) = + 1.25*(0) - (5*(0 - 0)/1.5*(0 - 0))/2*(0 - 0)*(1/3) = 0 (кН*м)
M1(1.50) = + 1.25*(1.50) + (5*(1.5 - 0)/1.5*(1.50 - 0))/2*(1.50 - 0)*(1/3) = 0 (кН*м)
Локальный экстремум в точке x = 0.87:
M1(0.87) = + 1.25*(0.87) - (5*(0.86625 - 0)/1.5*(0.87 - 0))/2*(0.87 - 0)*(1/3) = 0.72 (кН*м)
Рассмотрим второй участок 1.5 ≤ x2 < 3
Поперечная сила Q:
Q(x2) = + RA - (U1справа *1.5)/2 + ([(U2слева - U2слева *(3 - x)/1.5)*(x - 1.5)]/2 + U2слева *(3 - x)/1.5*(x - 1.5))
Значения Q на краях участка:
Q2(1.50) = + 1.25 - (5*(1.5 - 0)/1.5*(1.50 - 0))/2 + ([(5 - 5*(3 - 1.5)/1.5)*(1.5 - 1.5)]/2 + 5*(3 - 1.5)/1.5*(1.5 - 1.5)) = -2.50 (кН)
Q2(3) = + 1.25 - (5*1.5)/2 + ([(5 - 5*(3 - 3)/1.5)*(3 - 1.5)]/2 + 5*(3 - 3)/1.5*(3 - 1.5)) = 1.25 (кН)
На этом участке эпюра Q пересекает горизонтальную ось. Точка пересечения:x = 0.63
Изгибающий момент M:
M(x2) = + RA*(x2) + (U1справа *1.5)/2*(x - 1.5 + (1/3)*1.5) - ([(U2слева - U2слева *(3 - x)/1.5)*(x - 1.5)]/2*(x - 1.5)*(2/3) + U2слева *(3 - x)/1.5*(x - 1.5)*(x - 1.5)*(1/2))
Значения M на краях участка:
M2(1.50) = + 1.25*(1.50) + (5*(1.5 - 0)/1.5*(1.50 - 0))/2*(1.50 - 0)*(1/3) + ([(5 - 5*(3 - 1.5)/1.5)*(1.5 - 1.5)]/2*(1.50 - 1.5)*(2/3) + 5*(3 - 1.5)/1.5*(1.5 - 1.5)*(1.50 - 1.5)*(1/2)) = 0 (кН*м)
M2(3) = + 1.25*(3) + (5*1.5)/2*(3 - 1.5 + (1/3)*1.5) - ([(5 - 5*(3 - 3)/1.5)*(3 - 1.5)]/2*(3 - 1.5)*(2/3) + 5*(3 - 3)/1.5*(3 - 1.5)*(3 - 1.5)*(1/2)) = 0 (кН*м)
Локальный экстремум в точке x = 0.63:
M2(2.13) = + 1.25*(2.13) + (5*1.5)/2*(2.13 - 1.5 + (1/3)*1.5) - ([(5 - 5*(3 - 2.13375)/1.5)*(2.13375 - 1.5)]/2*(2.13 - 1.5)*(2/3) + 5*(3 - 2.13375)/1.5*(2.13375 - 1.5)*(2.13 - 1.5)*(1/2)) = -0.72 (кН*м)
Расчет произведен при помощи онлайн-сервиса SOPROMATGURU.RU